(For DC Network)
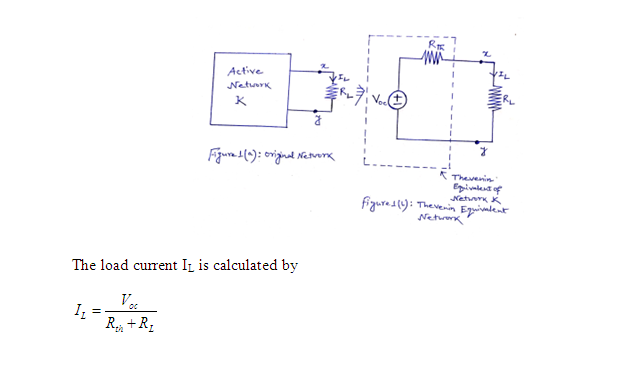
A linear two terminal active dc network K consisting of independent and/or dependent voltage and/or current sources and resistors can be replaced at a pair of terminals x-y by an equivalent network consisting of a voltage source Voc in series with a resistance Rth.
The voltage source Voc is the voltage across the terminals x-y when they are open circuited. This voltage is called the Thevenin equivalent voltage or Thevenin open circuit voltage.
The Thevenin equivalent resistance Rth has a value given by the ratio of the open circuit voltage Voc and the short circuit current Isc at the terminals x-y of the original network K. That is

If all the sources are independent, the Thevenin equivalent resistance Rth is the total resistance at the open-circuited terminals x-y when all ideal voltage sources are replaced by short circuits and all ideal current sources are replaced by open circuits.
Consider a linear active network K connected to a load resistance RL as shown in Figure 1(a). To determine the current through or voltage across load resistance RLconnected between the terminals x-y, the rest of the network may be replaced by a simple equivalent network consisting of Voc in series with Rth [see Figure 1(b)].
Problem 1: Find the current in 5 Ω resistor in the circuit of Figure 2 using Thevenin’s theorem.

Solution: First disconnect 5 ohm resistance in Figure 2 and determine open circuit voltage Voc and Thevenin’s equivalent resistance Rth across a-b.
To find open circuit voltage Voc [see Figure 2(a)]
Assume current flowing in loop be i. Apply KVL in the loop in clockwise direction,

To find Thevenin’s equivalent resistance Rth [see Figure 2(b)]


Problem 2: Find the current through resistor RL in the circuit of Figure 3 using Thevenin’s theorem. Consider RL=2 Ω, 4 Ω, 6 Ω, 8 Ω, and 10 Ω.

Solution: First disconnect RL in Figure 3 and determine open circuit voltage Voc and Thevenin’s equivalent resistance Rth across x-y.
To find open circuit voltage Voc [see Figure 3(a)]

We can solve by two methods.
Method I: Here 12 V voltage source is connected in series with 6 Ω resistor [See Figure 3(a)]. Converting 12 V source into equivalent current source of magnitude 2 A (12V/6Ω) [See Figure 3(b)]. From Figure 3(b), both 2 A current sources are connected in parallel and in same upward direction. Their equivalent magnitude is 4 A [See Figure 3(c)]. Converting 4 A current source into equivalent voltage source, the value of the voltage source is 4×6=24 V. [See Figure 3(d)].

Method II: Here one 12 V voltage source and one 2A current source are present [See Figure 3(a)]. We apply Superposition theorem in Figure 3(a) to solve Voc. We consider one source at a time and remove other source.
Now 12V voltage source acting alone and removing 2A current source by open circuited [see Figure 3(e)].

Now 2A current source acting alone and removing 12V voltage source by short circuited [see Figure 3(f)]. Converting 2 A current source into equivalent voltage source, the value of the voltage source is 2×6=12 V. [See Figure 3(g)].

To find Thevenin’s equivalent resistance Rth [see Figure 3(h)]



Problem 3: Find the Thevenin equivalent of the circuit in Figure 4 at terminal x-y.

Solution: In this circuit one dependent source is present, unlike the circuit in the previous problems.
To find open circuit voltage Voc across x-y [see Figure 4(a)].









