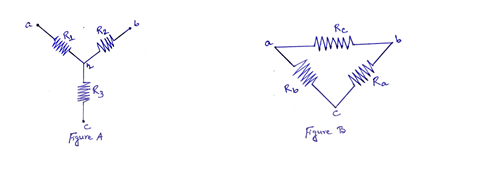
The resistances may be connected in star (or T or wye) or delta (or Δ or π) connection like series and parallel connections as shown in Figure A (Wye connection) and Figure B (Delta connection).
Delta to Wye Conversion
The formulas for a delta to wye transformation are (See Figure A)
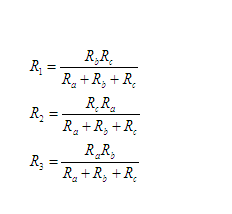
Wye to Delta Conversion
The formulas for a wye to delta transformation are (See Figure B)
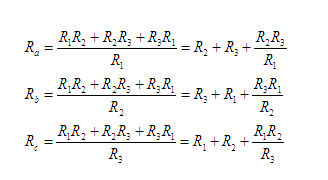
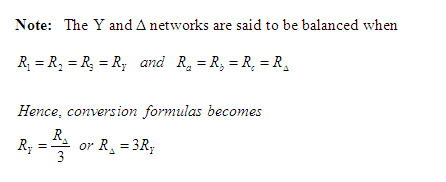
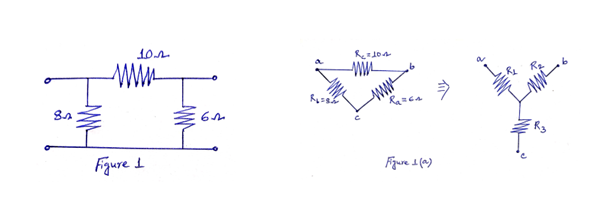
Problem 1: Convert the π network shown in Figure 1 into equivalent T network.

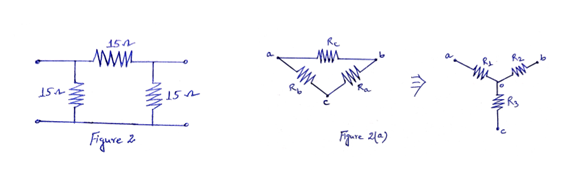
Problem 2: Convert the π network shown in Figure 2 into equivalent T network.

Problem 3: Convert the T network in Figure 3 to a delta network.
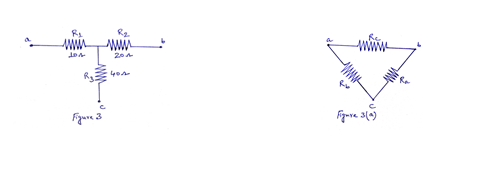

Problem 4: Find the equivalent resistance R of the network shown in Figure 4.
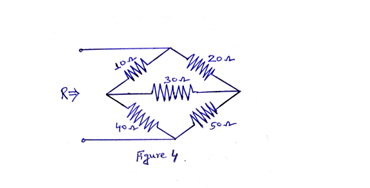
Solution: The network in Figure 4 can be redrawn as shown in Figure 4(a).
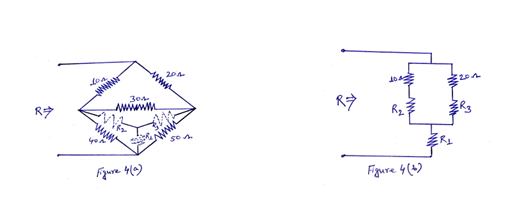
Here, R1, R2 and R3 in star combination represent the equivalent of the given lower delta network. Hence,
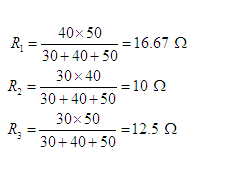
Next we modified the network as shown in Figure 4(b). Hence, the equivalent resistance R of the network can be written as
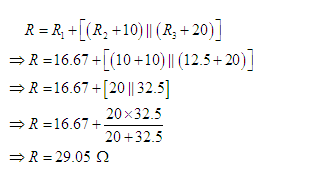
2nd Approach
The network in Figure 4 can be redrawn as shown in Figure 4(c).
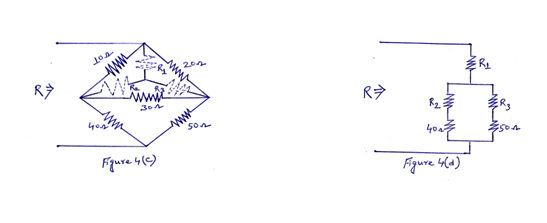
Here, R1, R2 and R3 in star combination represent the equivalent of the given upper delta network. Hence,
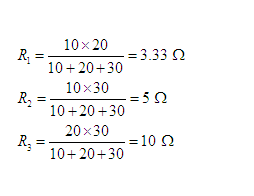
Next we modified the network as shown in Figure 4(d). Hence, the equivalent resistance R of the network can be written as
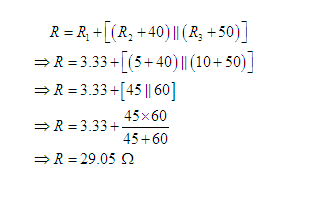
Problem 5: Find the equivalent resistance R of the network shown in Figure 5.
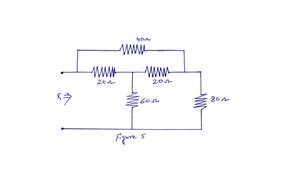
Solution: Convert the T connected network using 20 Ω, 20 Ω and 60 Ω resistors to an equivalent delta network [see Figure 5(a)].
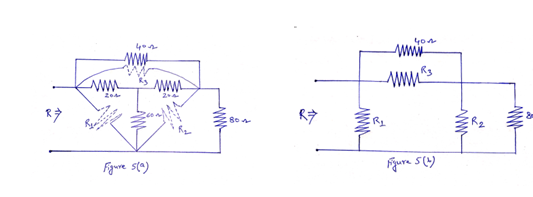
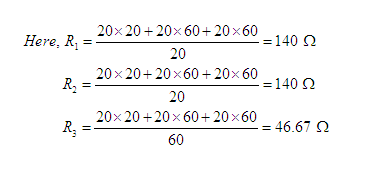
Next we modify the network as shown in Figure 5(b). Here R3 and 40 Ω are connected in parallel. Their equivalent resistance is 21.53 Ω.
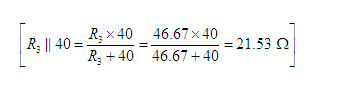
Now R2 and 80 Ω are connected in parallel. Their equivalent resistance is 50.9 Ω.
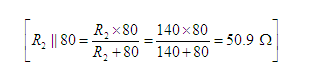
Here 21.53 Ω and 50.9 Ω are connected in series. Their equivalent resistance is 72.43 Ω [21.53 Ω+50.9 Ω].
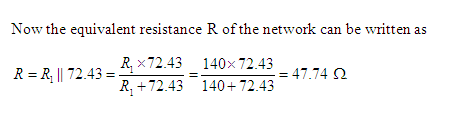
2nd Approach
The network in Figure 5 can be redrawn as shown in Figure 5(c).
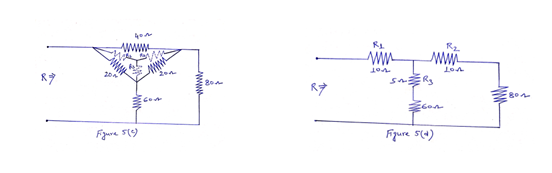
Here, R1, R2 and R3 in star combination represent the equivalent of the given delta network. Hence,
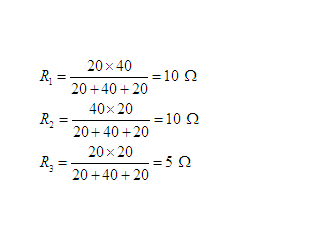
Next we modified the network as shown in Figure 5(d).
