Mesh Analysis (or Loop Analysis or Mesh Current Method)

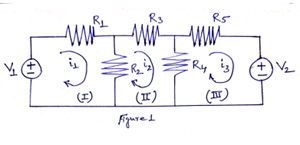
Let us consider the network shown in Figure 1. It consists of three loops [Loop (I), loop (II) and loop (III)]. The three loop currents are i₁, i₂ and i₃ and they are assumed to flow in a clockwise direction. Here, the currents in different loops are assigned continuous paths so that they do not split at a junction into branch currents. The mesh analysis or loop analysis is based on Kirchhoff’s voltage law (KVL). Here in this method three loop currents i₁, i₂ and i₃ are unknown quantities.

Apply KVL in loop (I) in clockwise direction,

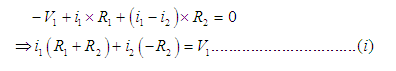
Apply KVL in loop (II) in clockwise direction,

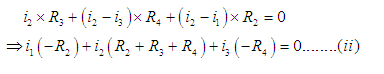
Apply KVL in loop (III) in clockwise direction,

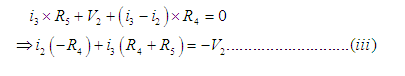
Solving equations (i), (ii) and (iii), we can find the values of  i₁, i₂ and i₃.

Equations (i), (ii) and (iii) can be written in matrix form as

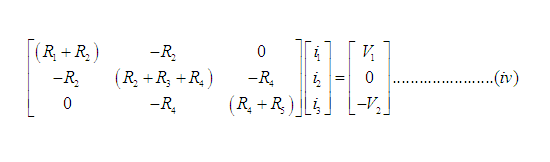
In general, the resistance matrix [R] can be written as

Where

R₁₁=self resistance of loop (I)=R₁+R₂

R₂₂=self resistance of loop (II)=R₂+R₃+R₄

R₃₃=self resistance of loop (III)=R₄+R₅

R₁₂=R₂₁=-[sum of all the resistances common to loops (I) and (II)] =-R₂

R₂₃=R₃₂=-[sum of all the resistances common to loops (II) and (III)] =-R₄

R₁₃=R₃₁=-[sum of all the resistances common to loops (III) and (I)] =0

Here, R₁₁, R₂₂ and R₃₃ are called diagonal elements while R₁₂, R₁₃, R₂₁, R₂₃, R₃₁ and R₃₂ are called off-diagonal elements of the resistance matrix [R].

From equation (iv), the values of i₁, i₂ and i₃ can be solved by Cramer’s rule. From equation (iv), we can find out the determinants D, D1, D2 and D3 which are given in equations (vi), (vii), (viii) and (ix).

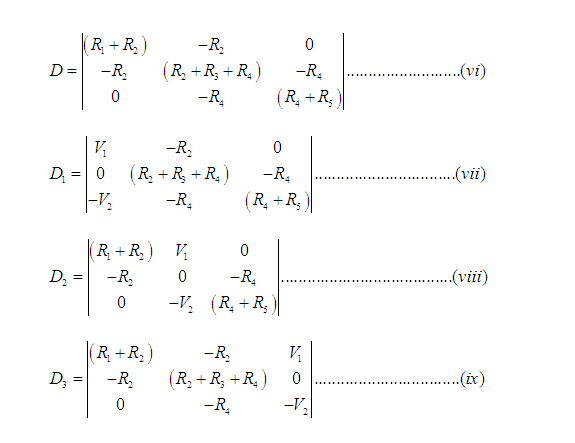
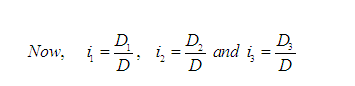
In these way, we can find the values of  i₁, i₂ and i_3.

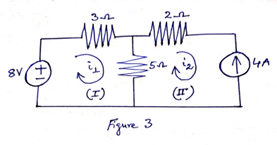
Problem 1: Find the branch current i₁, i₂ and i₃ using mesh analysis in Figure 2.

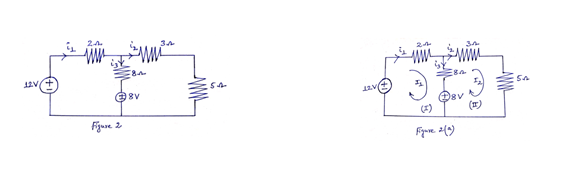
Solution:

Method 1:

Here, there are two loops [Loop (I) and loop (II)]. Assume current flowing in loop(I) and loop(II) are I₁ and I₂ respectively. [See Figure 2(a)]

Apply KVL in loop (I) in clockwise direction,

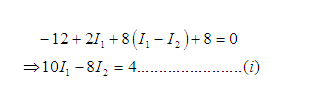
Apply KVL in loop (II) in clockwise direction,

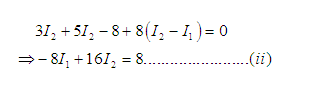
Solving (i) and (ii),

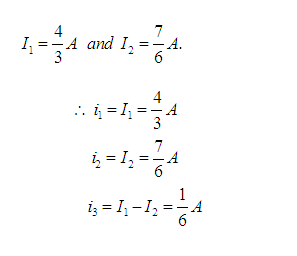
Method 2: Use Cramer’s rule.

From Figure 2, we can write

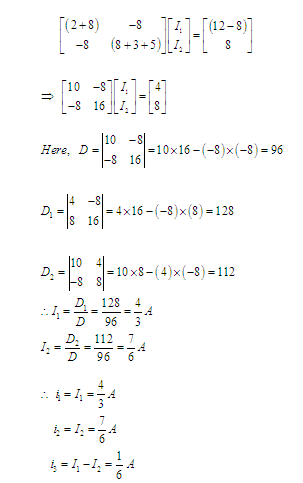
Mesh Analysis with Current Sources

Consider the following two possible cases.

CASE 1: When a current source exists only in one mesh

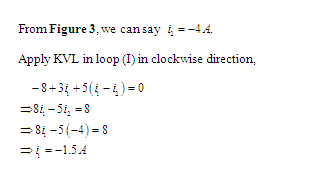
CASE 2: When a current source exists between two meshes

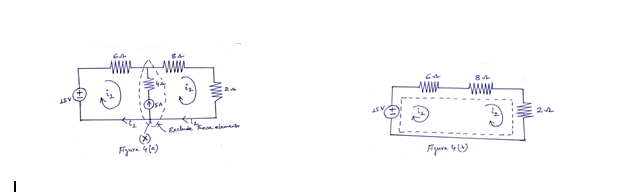
Consider the circuit in Figure 4(a). We create a supermesh by excluding the current source and any elements connected in series with it [see Figure 4(a)].

A supermesh consists of two meshes that have a current source (dependent or independent) in common.

Apply KVL to the supermesh in Figure 4(b) gives

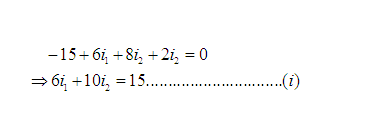
We apply KCL to a node in the branch where the two meshes intersect. Apply KCL to node (X) in Figure 4(a) gives

Solving (i) and (ii) gives

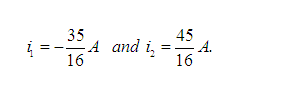
Important Points to Remember :

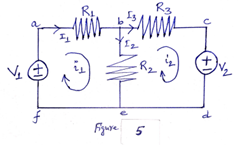
• A mesh is a loop which does not contain any other loops within it.  A loop is a closed path with no node passed more than once. Paths abefaand bcdeb are meshes, but path abcdefa is not a mesh [See Figure 5]. The current through a mesh is known as mesh current. We are applying KVL to find the mesh currents in a given circuit. Although path abcdefa is a loop (not a mesh) and we can apply KVL here also. This is the reason for loosely using the terms loop analysis and mesh analysis. We can apply mesh analysis to planar circuits only. A planar circuit is one that can be drawn in a plane with no branches crossing one another.
• A supermesh requires the application of both KVL and KCL.